Shuffling around Expected Value

A simple proof that we should (typically) maximize expected value

Years ago, in ‘Expected Value without Expecting Value’, I noted that “The vast majority of students would prefer to save 1000 lives for sure, than to have a 10% chance of saving a million lives. This, even though the latter choice has 100 times the expected value.”

Joe Carlsmith’s essay on Expected Utility Maximization nicely explains “Why it’s OK to predictably lose” in this sort of situation. The argument I find most compelling draws on the principle that it shouldn’t matter if we just move people around in probability space. But we can start with a scenario in which we obtain the expected value with certainty, and harmlessly shuffle people around to reach more “risky”-seeming prospects with that same expected value. Let me explain.

Shuffling Prospects across Boxes

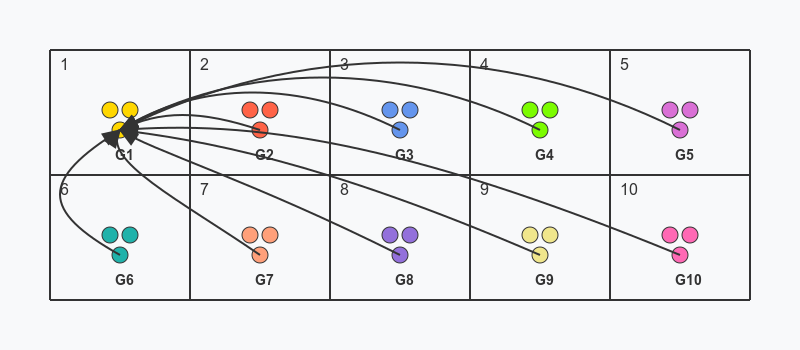
Suppose you could save 100k lives for certain. That would be amazing! (Clearly way better than just saving 1k.) To make it more precise, suppose that one million at-risk lives are split into ten equal groups, G1 to G10, of 100k people each. A ten-sided die is rolled, and whichever number n lands, the corresponding people in the nth box are saved. So, whatever the roll, exactly 100k people will be saved (though a different group depending on the roll).¹

Now notice that it doesn’t matter, to the members of each group, which box they are in (prior to learning the result of the die roll): they have a 10% chance of survival regardless. G2 might as well move to square 1 (and so be saved if the die lands 1 rather than 2), and likewise for the other groups. But that’s just to say that a 10% chance of saving 1 million people is morally equivalent to the above-described way of saving 100k people with certainty, so far as the affected people themselves are concerned.

Thanks to Claude for making this neat illustration!

In this case, we should simply care about the people in the situation. So if the pre-move and post-move prospects are equivalent from the perspective of all involved (as, we’ve seen, they are), then we should conclude that the two prospects are morally equivalent. A 10% chance of saving 1 million people (which otherwise, with 90% probability, saves nobody at all) is morally equivalent to saving 100,000 people with certainty.

We could similarly run the argument with smaller groups distributed across 100 boxes (or 1000), representing just a 1% (or 0.1%) chance of saving everyone, to see that this lower chance of success is morally equivalent to saving 10,000 people (or 1000 if we instead use the bracketed numbers) with certainty. It really doesn’t matter how small the probabilities get: the basic logic of how to think about expected value doesn’t change. So long as we’re really talking about well-grounded probabilities, it’s irrational to outright ignore small probabilities, because that amounts to caring about how prospects for independent groups are clustered. And that isn’t something that it (typically) makes any sense to care about.

If your reason for rejecting a higher-EV action is solely that it has a higher probability of saving no-one at all, then you are failing to be guided by moral consideration for the individuals whose lives are at stake. You’re almost certainly doing something more selfish, like anticipating how you will feel bad and regretful when the die picks out a square that happens to be empty. The clustered (post-move) distribution is worse for you, in this way. But your feelings in this matter are utterly trivial compared to saving an extra 99,000 lives in expectation. It is not morally decent to let your anticipated regrets swamp so many others’ lives in your decision making. (If you had better-calibrated emotions, you’d feel 100x more positively about saving 100x more lives, but of course our emotions just don’t work like that. So be aware that your emotions are stupid and systematically lead you astray in this way.)

How Clustering Can Matter

The above form of argument works when we should simply care about the lives at stake in the situation. But not all cases meet this condition. Raise the stakes high enough—make it so that G1 - G10 represent the entirety of humanity, for example—and the payoffs change. When G2 moves to box 1, leaving box 2 empty, this now creates a real difference: a chance of total human extinction. If the other groups follow suit, leaving us with a 90% chance of extinction, that is vastly worse than a guarantee of precisely 10% of the population surviving. (Assuming, at least, that 10% of the population is enough for civilization to persist and rebuild.)

This reveals something very important. When thinking about expected value “fanaticism”, philosophers typically diagnose the problem as stemming from giving weight to excessively small probabilities. But the shuffling boxes argument decisively proves that there’s no essential problem with giving proportionate weight to low probabilities of positive outcomes. There’s nothing fanatical about accepting a mere reshuffle or movement of beneficiaries across probability space, when nothing else is at stake. Rather, what’s intuitively “fanatical”, to my way of thinking, is to risk (a sufficiently high probability of) unacceptable losses—losses, like human extinction, which go beyond the interests of the particular individuals in the situation. This explains why it makes sense to care about clustering in such cases.

Compare “Double or Nothing” Existence Gambles. This seems like a form of expected-value “fanaticism” if anything is, yet the probably of success is at least 50%! The problem isn’t the probabilities, but the payoffs: we’re supposed to imagine that doubling the basic goods makes for an outcome with double the value. But this just doesn’t seem credible. The loss of everything good in the world would be a loss of far greater magnitude (or moral significance) than the gain from doubling everything good. Intuitively, we should highly value adequate outcomes, and not easily be willing to risk everything for mere “luxury” benefits beyond that. It’s not entirely obvious how to theoretically accommodate this intuition (some kind of diminishing marginal value for basic goods may be the most promising route, though it is not without challenges of its own). But it strikes me as a more respectable intuition—more worth seeking to accommodate, perhaps—than the “round down small probabilities to zero” idea.

Proves too much?

What if someone were to try to take this mode of response and apply it to our starting case? Could they argue that having all one million people die (with 90% probability) is “unacceptably risky”, and so we should care about the clustering to such an extent as to prefer to save even 1000 people over a 10% chance of saving one million?

One could certainly say this. The question, as always in ethics, is whether the claim is really credible or substantively plausible. I think it would not be. Against a background population of billions, it’s just not clear why we would have disproportionate reason to care about just 1000 out of one million at-risk lives surviving in this case. It would seem far more principled to value everyone equally in this case, and so recognize both that (i) saving 100x as many people really would be 100x better, and (ii) there’s no strong moral reason to care about how the chances of rescue for each group are clustered (i.e. whether the groups are spread across the entire grid of probability space, or all squeezed into a single square). You need a positive reason to care about the clustering; otherwise, the default should be to just care about the individuals’ perspectives. And we’ve already seen that the clustering makes no difference to them.² So we should not care about it either (without good reason).

A practical proviso:

I have assumed throughout the above that we’re talking about objective probabilities which are themselves known for certain. As I explain in Risk Aversion as a Humility Heuristic, in real-life cases we may reasonably discount small probabilities due to asymmetric risks from miscalibration (the potential costs from overestimation may swamp the potential benefits in the event of underestimation, especially if there are reasonable grounds for suspecting that a first-pass probability estimate for a weird or ‘Pascalian’ possible outcome is likely to be an overestimate). Those sorts of “non-ideal decision theory” considerations are extremely practically important, but don’t speak to the “in principle” merits of expected value reasoning—i.e., in ideal theory—that the current post is concerned to address.

1. I assume that it is at least not worse to give everyone an equal chance of being saved, compared to an alternative implementation in which the same 100k people will be saved (and the other 900k are condemned to death) no matter what.

2. This may be a slight oversimplification. If anything, the at-risk individuals may benefit from greater clustering, as they then don’t risk “survivor’s guilt”: when they survive, so does everyone else who was at risk! But that would subtly change the payoffs, so we bracket such complications in order to make the underlying logic of the situation easier to follow.